If youíve been following this series, you know that Iíve been moving inexorably toward a computer simulation of racing. Iíve repeatedly debated with myself writing a new one completely from scratch versus starting with someone elseís work. Ten years ago, when I started this series, the choice was easy. Since there was nothing out there, I had to start from scratch. The situation has changed. There is at least one competently executed program in the public domain.
Doing a derivative work has undeniable advantages, but conflicts with one of the enduring goals of this series, that is, to do totally original work rather than to recapitulate information you can get from other sources. However, one has to start somewhere. After all, it would be silly for me to rediscover Newtonís laws, so I take those as given. Likewise, Iíve concluded that it would be silly for me to invent the infrastructure for a simulation. It would be a very long digression indeed from the Physics of Racing to cover all the groundwork such as
memory management, windowing, graphics, rendering, data reporting, etc.
programming languages, scripting, object technology
simulation technology: time-stepping, eventing, dynamics solvers
data structures for track description and cars
arbitrary choices for coordinate systems
All this, while interesting, is not physics. Furthermore, nowadays, itís all more-or-less conventional technology. Itís not terribly important for us to make choices in these domains if we can find a competent base platform in which reasonable choices have already been made.
So, with only a little reluctance, I take the decision to start with an existing program. My choice is RARS, the Robot Auto Racing Simulator. This is a lovely, surprisingly simple platform for programmers to experiment with robotics. Its purpose is to support distributed virtual racing competitions, in which entrants write robot drivers and enter them in planned events. The last competitions I have been able to find on the web were conducted in 1999. It is not a high-fidelity simulation, and, in fact, was never intended to be. Its physics is simplified in a very clever way to make the main challenge for competitors the writing of robots rather than struggling with elaborate, high-fidelity physics. It supplies a working infrastructure and a large amount of decent data describing famous tracks. Finally, so far as I can tell, RARS is in the public domain.
The simplifications in RARS make it the perfect starting point for enhancing the physics without having to reinvent the peripheral aspects of a simulation program. Note that RARS was designed for public contribution: the program was originally made to be easy to modify. The usual mode of modification is for competitors to add new robots. However, it is just as easy to change the physics, as I intend to do. Now, as I take the program in new directions, I will either have to modify the robots or, possibly, create a new, public racing series and throw open the writing of new robots to everyone. Only time will tell what works out best. As usual, however, I will make changes incrementally, never deviating very much from the working base. This strategy will not only keep the changes under control, but also enable me to explain to you whatís going on, step-by-step.
Therefore, I will create a copy of the sources and change the name of my copy to RARSEP, for " RARS, Enhanced Physics" . I will post the source code of my changes on the web to keep the new project rolling along.
My first, long-term goal with RARSEP is to find optimal racing lines. In particular, I need a way to answer questions about racing lines, such as whether the shortest line or the highest-speed line around a particular feature results in the lowest time around the entire course, that is, with the feature in context. Such a question is part of " reading a course" , one of the tasks of every racer. In practice, this is a trial-and-error process involving folklore, experience, and experimentation.
For instance, at a recent track day I attended, two instructors, each with many hours on this particular course, were debating a certain combination of slow corners. After quite a bit of haggling and white-board hacking, they agreed that the classic line they had been taking for years was probably not the fastest line. It will warm the hearts of autocrossers to find that they had discovered that the autocrosser line, rather than the class road-racer line, was probably fastest.
Autocrossers spend most of their effort finding the fastest way around slow corners, whereas the primary challenge for road-course drivers is finding the fastest way around fast corners. There is no end of reading material supporting the classic, road-racing lines: enter as wide as possible (or, as high, as one would say in NASCAR), trail-brake, get back on the throttle in the first half, squeeze on the gas, look up, late apex, and track out. As often as not, however, autocrossers find that simply hugging the inside as tightly-as low-as possible yields the quickest way around. Why? Is there science behind this? Can they both be right? How about both wrong? What about intermediate cases: medium-slow and medium-fast corners?
That is an example of the kind of question that we want to answer with a simulation program. It was interesting that the instructors' debate concerned slow corners. No one was debating that the fast corners should be taken classically. But, and here I hypothesize, slow corners have the characteristic that the corner is not very much larger than the car. Could it be that when this is true the classic racing line is suboptimal? Experienced autocrossers would, when coming up on such corners, without even thinking about it, go in low and tight and just carry speed or toss-and-catch the car. The instructors had, following the classic theory, been going in high and wide, turning in late, and thereby wasting time trying to form a classic line around corners not much bigger than the car. But, could it be that the classic theory is not best when a corner is so small that the wheelbase of the car is a significant fraction of the distance around the corner? Maybe there are other factors, though. Could it be that the size of the corner does not suffice to distinguish an " autocrossy" corner from a " road-racey" corner? Does context matter, as in whether the corner is near other corners or near straights?
It seems that even the most experienced drivers of a particular track will occasionally discover improvements to the line. Some of these improvements depend on transient conditions like weather or the particulars of a certain car or setup. Lots of tracks have canonical " rain lines" that differ from the " dry lines" . I would also bet that Winston Cup cars take different lines around Sears Point and Watkins Glen than do ground-effects sports cars and downforce formula cars. But some improvements will be deep, permanent, invariant revelations that may have eluded the racer on previous outings and analysis. That, in a nutshell, is the first place weíre going with RARSEP: to have a way to answer such questions.
I will start with the Windows port of RARS version 074, which you can get in source and binary forms from the following web sites:
I choose the Windows port because itís most convenient for me: I already have working development systems on Windows, whereas to work on other platforms would entail ramp-up time and money. The RARS code base is currently portable to multiple platforms, including Linux and Windows. The code is very well partitioned, so that the platform-dependent bits are separated from the platform-independent bits. Everything I intend to do will be in the platform-independent parts of the program and should build without difficulty on all the platforms. However, I will not be able to test my changes on all platforms - the Physics of Racing is not an exercise in industrial-strength, portable software development. While I have no intention of making non-portable changes, there is a small risk that I might inadvertently do so and it could happen some files might someday need a little tweaking to get going on other platforms. I am sure my readers will let me know about it.
The web sites contain very complete descriptions of how to build and run the program, plus how to write robots. To write a robot, one needs to understand the existing physics model of RARS. Similarly, to enhance the physics, we'll need to know the same thing. It presently appears that the best way to enhance the physics incrementally will be in the context of writing a robot, but this may change as we dig in. The subject of this instalment of the Physics of Racing will therefore be to introduce the existing RARS physics model along with a long-range plan for enhancing the physics. I am very grateful to the authors for supplying RARS and I hope they will enjoy what I do with their work. The program is very easy to build, run, understand, and enhance. I encourage you to download it and follow along with me. However, my articles will be self-contained: you wonít need to build and run RARS to understand what Iím doing with it.
I have found that there is another independent effort afoot to enhance RARS. It's called TORCS and can be found at http://torcs.free.fr/. This includes some of the enhancements I intend to make, but its goals are like those of RARS rather than like mine. It looks very promising, but it has three features that make it unsuitable as a starting point for me:
it's unfinished, whereas RARS is functional and established
it's Linux-based. I donít have a Linux development environment, and it would take me too much time and money to build one up at present
as usual, peeking (too much) at other work would spoil the fun for me
However, I will be keeping an eye on TORCS. It may turn out to be terrific!
My first approach to adapting RARS to a line-finding task will be to write a robot that learns the optimal line by making small modifications on each lap around the track, much as a human driver would do. This is a kind of variational approach, common in physics. The line-finding robot (LFR) will build an internal memory of its current line and everything it discovers about the track. Then, it will tweak the line, and, if the lap time goes down, continue to tweak in the same direction. Otherwise, it will discard the tweak and try another. At the point of diminishing returns, it will start tweaking another part of the line.
Itís going to consume a lot of computing resources and not be competitive in the real-time setting of the old RARS. However, remember, with RARSEP, we are changing the goals. Also, this plan may take considerable time and span many articles. It may not work out at all. As usual, I am taking you along for the ride.
So, let's describe the current physics model. RARS' algorithm is devilishly simple, just the right compromise between physics rich enough to be convincing yet not so complicated that writing a robot is too challenging. Every time step, the simulation engine gives each robot a situation structure, and the robot responds with a command or control structure. The situation structure contains the current location and velocity of the car relative to the track, the walls, and the other cars. The control structure declares the desired slip angle - roughly representative of the steering-wheel angle - and the desired forward velocity - roughly representative of the throttle (positive) and brake (negative). The controls interact with the road through a tyre friction model, generating a force that accelerates the car. The force is limited by the power available from the engine, so, it is not always the case that all the force the tyres could deliver can be applied, since the engine may not be able to pump it out. So, the desired velocity may not be the achieved velocity.
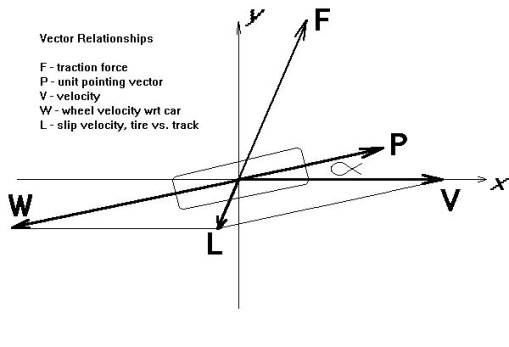
One reason that RARS is simple is that it is two-dimensional. In 2-D RARS, there are three, right-handed coordinate systems. First is the ground, a nearly inertial coordinate system fixed with respect to the road. Forces and accelerations are computed in this system, since it is inertial. Second is the car coordinate system. The x-axis of car points forward and the y-axis points to driverís left. Third and final is the path coordinate system, aligned with the carís velocity vector. The tangential component of any vector points along the x-axis of path, and the normal component of any vector points along the y-axis of path. Car aligns with path only when the car has no slip angle.
The following table, adapted from the program documentation, summarizes the physics model:
| V | = car's velocity vector WRT (with respect to) ground |
|---|---|
| v | = ground speed = magnitude of V |
| P | = forward-pointing unit vector in the car system |
| alpha | = " slip angle" [command output from robot], which separates P and V. Alpha is positive when the car points to the left of V, as when power-sliding around a left-hand corner. |
| W | = velocity vector of tyre contact patch WRT car, always points backwards along x axis |
| vc | = " velocity commanded" , [command output] forward in the car system W = -P * vc |
| L | = V + W = V - P * vc = " slip vector" , velocity of contact patch WRT ground |
| Lt | = path-tangential component of L = v Ė vc * cos(alpha) |
| Ln | = path-normal component of L = v - vc * sin(alpha) |
| l | = slip speed = magnitude of L |
| Q | = L / l = unit vector in the direction of L |
| mu(l) | = coefficient of friction, depending only on slip speed |
| F | = - Q * mass * mu(l) = force vector pushing the car, in the direction opposite to L |
| f | = mass * mu(l) = magnitude of F |
| Ft | = path-tangential component of F = - f * Lt / l |
| Fn | = path-normal component of F = - f * Ln / l |
| FtP | = projection of Ft in the car system = Ft * cos(alpha) |
| FnP | = projection of Fn in the car system = Fn * sin(alpha) |
| pwr | = engine power consumed = sum of force components along P limited by engine capacity = max(181hp, (FtP + FnP) * vc) |

The friction function currently used is of the form u(l) = FMAX * l / (K + l) where FMAX and K are given constants.
To summarize the limitations of the current model:
Planned enhancements:
As we progress, it may be helpful to keep these pages around. We will refer to them frequently.